The Spanish CRG BM25B - SpLine beamline is dedicated to structural investigations using hard X-ray scattering mostly in materials science, specialized on X-Ray diffraction techniques and hard X-ray photoemission spectroscopy.
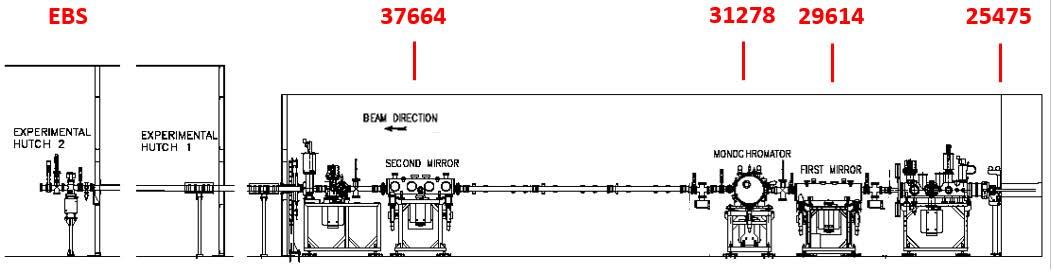
BM25B is located on the hard edge of the bending magnet D25 with a critical energy of 20.6 keV. The optics accepts 2 mrad of the horizontal radiation fan and produces a small focal spot at different positions (B1 and B2) in the experimental hutch B. The beamline is intended for Single Crystal Diffraction (SCD), Grazing incidence X-ray diffraction (GIXRD), Surface and Interface X-Ray Diffraction (SXRD), X-ray reflectivity (XRR) and Hard X-Ray Photoelectron Spectroscopy (HAXPES). At SpLine, we have developed a novel set-up that combines HAXPES and x-ray diffraction (surface/interface and bulk x-ray diffraction, and x-ray reflectivity). Both techniques can be operated simultaneously on the same sample using the same excitation source.
Grazing incidence and single crystal X-Ray diffraction station
The main objective of this end-station is to provide a large variety of X-ray diffraction experiments for the Spanish scientific community, as well as for foreign scientists around the world. An important aspect, which has been one of the major goals of the end-station during the design, start-up and upgrade periods, is the adaptability and flexibility for different sample environment set-ups that must be easily installed to allow for a high throughput of users. It is conceived to carry out X-Ray Reflectivity (XRR), Surface X-Ray Diffraction (SXRD), Single Crystal Diffraction (SCD), Reciprocal Space Maps (RSM), Grazing Incidence X-Ray Diffraction (GI-XRD) and High Resolution Powder Diffraction (HRPD) experiments. Thus, the multipurpose character of the end-station is reflected on the huge variety of experiments carried out in the last years, showing multidisciplinary work areas, from surfaces and thin films to liquid crystal materials.
The multipurpose X-ray diffraction set-up is mainly composed of a six-circle diffractometer in vertical geometry equipped with a 2D MaxiPix detector placed on the diffractometer arm and a CCD detector mounted on an independently motorized stage. The sphere of confusion for the whole collection of circles is 50 μm. There are many experiments that can be carried out on this multipurpose diffractometer. Among them, the study of surface and buried interfaces morphology on thin and ultra-thin films are predominant. The possibility to perform high resolution reciprocal space maps (RSM) in combination, under the same set-up, with low- and high-angle XRR and with Surface and Interface X-ray Diffraction enables a unique method for a complete structural and morphological characterization of thin films and multilayers.
Surface X-Ray Diffraction, Grazing incidence X-ray diffraction, X-ray reflectivity and Hard X-Ray Photoelectron Spectroscopy Station
The second focal point on Branch B hosts a state-of-the-art set-up dedicated to the simultaneous combination of X-ray Diffraction and Hard/Soft X-ray Photoelectron Spectroscopy. Such a set-up offers the unique possibility to correlate the atomic structure of the sample with its compositional, chemical and electronic properties. This is of particular importance for many systems, such as complex oxides or topological insulators, i.e., strongly correlated electron systems, for which their macroscopic properties are intimately related to an intricate interplay between charge, spin, and lattice degrees of freedom. Also the combination of X-ray reflectivity with hard and soft X-ray photoelectron spectroscopy is crucial for retrieving an accurate non-destructive compositional and electronic depth profile in the tens of nanometres depth-scale with nanometre resolution in amorphous, polycrystalline, single crystalline samples or hetero-structures. Furthermore, the ability to tune the excitation energy in the hard X-ray regime enables tuning the sampling depth, i.e. depth profile analysis, but also enables the discrimination between bulk and surface effects, especially if combined with variable incident angle and with soft x-ray excitation. Such a combination of techniques finds its optimal use in-situ experiments, .i.e., in-situ growth or in-situ treatment, as it is the only possibility to guaranty an accurate correlation between structural, compositional, chemical and electronic properties.
BM25
DCM Double-Crystal Monochromator
Hard X-ray Photoelectron Spectroscopy X-ray Surface Diffraction
Sample
Techniques usage
Manipulator or Sample stage
Sample Environment
Multipurpouse X-ray Diffraction
VHR 3x1 X-ray Camera
Manipulator or Sample stage
Sample Environment
2x2 MaxiPix
ESRF MAXIPIX device server
ESRF "Oxidis" image viewer
TANGO
SPEC runtime with ESRF macros (user interface)
Detection
FOCUS HV-CSA electron energy analyzer
resolution, which is of great importance to ensure excellent count rates and sensitivity at high kinetic energies. The FOCUS HV-CSA is a Cylindrical Sector Analyzer (CSA) with a slit to slit distance of 300mm.
It is designed to achieve optimum performance in a wide kinetic energy range between 1eV and 15keV.
Detection
VHR 3x1 X-ray Camera
ESRF VHRx3 device server
ESRF "Oxidis" image viewer
TANGO
SPEC runtime with ESRF macros (user interface)
Detection
- Crystallography
- Powder diffraction
- Surface diffraction
- Reflectrometry
- XPS
- Elastic scattering
- Wide angle scattering
ICMM - Instituto de Ciencias de Materiales de Madrid
CSIC - Consejo Superior de Investigaciones Científicas
71 avenue des Martyrs
38000 Grenoble, France
- SPEC
- Spectra, images (EDF),
- scii, edf
- PyMCA, ROD, UniFIT